Software: Turin

• Programm-Editor mit Syntaxprüfung
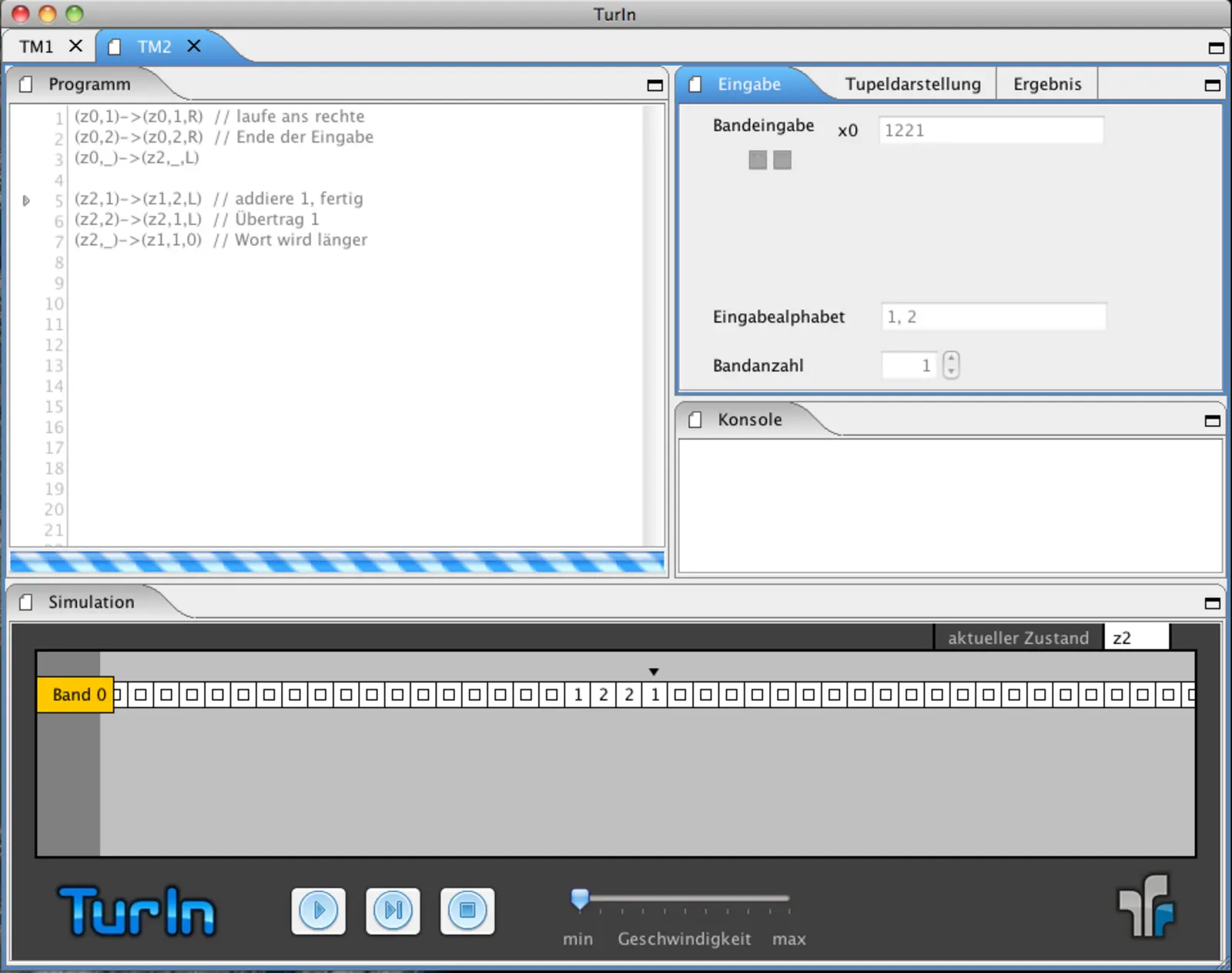
• schrittweise Simulation von Mehrband-Turingmaschinen gemäß diesem Opens internal link in current windowBerechnungsmodell
• graphische Darstellung der Arbeitsweise

Java Runtime Environment (Version 6, Update 23 oder höher)

Das Turin-Team besteht aus Studierenden und Mitarbeitern des Fachbereichs Informatik. An der aktuellen Version sind/waren beteiligt:
Marco Borkowitz, Michael Jokic und Paul Schiffgens

Wir freuen uns über Ihre Kommentare, Verbesserungsvorschläge, Fragen oder Fehlermeldungen. turin(at)informatik.hochschule-trier.de

Seien M=(Σ,Γ,Z,f,z₀,z₁) eine k-Band-Turingmaschine und w=a₀…a_n-1∈Γ\{_}. Die StartkonfigurationS(w) von M bezeichnet folgende Situation:

• die Steuereinheit ist in Zustand z₀,
• auf Band 0 steht a₀…a_n-1 mit Kopf 0 auf a₀ (falls n=0 steht der Kopf auf irgendeinem _),
• die Bänder 1,…,k-1 enthalten nur _.

Seien M=(Σ,Γ,Z,f,z₀,z₁) eine k-Band-Turingmaschine in Zustand z₁ und sei u∈Γ^∗ der Inhalt von Band 0 ohne führende und ohne nachfolgende Leerzeichen _. Dann ist das Berechnungsergebnis v von M das maximale Präfix v∈∑^∗ von u.

Sei m≥0 und sei M=(Σ,Γ,Z,f,z₀,z₁) eine k-Band-Turingmaschine. Die von M berechnete m-stellige Funktion φ_M:(∑^∗)^m→∑^∗ ist für alle x₀,…,x_m-1 definiert als 

• φ_M(x₀,…,x_m-1) = v, falls M in S(x₀∗x₁∗…∗x_m-1) startet und mit Ergebnis v anhält,
• φ_M(x₀,…,x_m-1) = n.d., falls M in S(x₀∗x₁∗…∗x_m-1) startet und nicht anhält.

Aus diesen Definitionen ergibt sich, dass φ_M(x₀,…,x_m-1) genau dann definiert ist, wenn M beginnend in S(x₀∗x₁∗…∗x_m-1) anhält.

Zustände werden in Turin stets mit zi bezeichnet, wobei i eine nichtleere Folge aus den Ziffern 0,...,9 ist. Start- und Stoppzustand sind als z0 bzw. z1 festgelegt.

Für das Bandalphabet Γ stehen höchstens die Symbole 0,…,9,a,…,z,A,…,Z zur Verfügung. Insofern ergibt sich im Unterschied zum Berechnungsmodell eine Maximalgröße für Γ.

Ein Übergang f(z,a₀,…,a_k-1) = (z',a'₀,…,a'_k-1,σ₀,…,σ_k-1) der Überführungsfunktion f mit z,z'∈Z, a_i∈Γ und σ_j∈{0,L,R} wird in Turin als Programmzeile

(z,a₀,…,a_k-1)->(z',a'₀,…,a'_k-1,σ₀,…,σ_k-1)

dargestellt. Beispiel für einen Befehl einer 2-Band-Turingmaschine:

(z0,2,1)->(z3,1,2,R,0)

Kommentare beginnen mit // und werden durch das Zeilenende begrenzt.

In Programmen dürfen unnötige Befehle der Einfachheit halber weggelassen werden, z.B. solche, die nie erreicht werden. Fehlt im Programm ein Befehl

(z,a₀,…,a_k-1)->

so verhält sich die Maschine entsprechend des gedachten Befehls

(z,a₀,…,a_k-1)->(z1,_,…,_,0,…,0).

Damit beschreiben auch unvollständige Programme immer totale Überführungsfunktionen.