Labor für Mathematik und Maschinelles Lernen

Mathematik ist eine fundamentale Disziplin des maschinellen Lernens und ist unerlässlich um

ein grundlegendes Verständnis dieses Wissenschaftsgebiets zu erlangen,
bestehende Verfahren weiterzuentwickeln und auf neue Anwendungen zu adaptieren,
Robustheit und Unsicherheit quantifizierbar zu machen,
das theoretische Fundament weiter auszubauen.

Das Labor für Mathematik und maschinelles Lernen dient der Durchführung von Projekten und Abschlussarbeiten zu Themengebieten des maschinellen Lernens. Ein besonderer Fokus liegt dabei auf Arbeiten mit Bezug zu den mathematischen Grundlagen und neuartigen Anwendungen neuronaler Netze.

Zum Projekt

Programmieren eines softwarebasiertes Dialogsystem, meist als Chatbot bezeichnet, zur KI-gestützten Beantwortung von Anfragen Studierender. Service Chatbot

Abschlussarbeiten

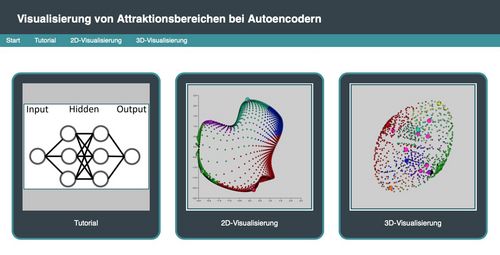
Neuronale Netze: Autoencoder

In neueren Untersuchungen zu neuronalen Netzen stellte sich heraus, dass Autoencoder die Tendenz aufweisen durch langes Trainieren Fixpunkte an Trainingsdaten auszubilden. Somit memorieren diese Netze gewisse Trainingsdaten ähnlich wie klassische Hopfield Netze.

Nicolas Schuler und Hendrik Büthe haben im Rahmen ihres Projektstudiums am Fachbereich Informatik eine Web-Applikation entwickelt, die es ermöglicht diesen Effekt und die Dynamik (iterative Anwendung von Autoencodern) anhand von 2D oder 3D Daten visuell begreifbar zu machen.

Zur App

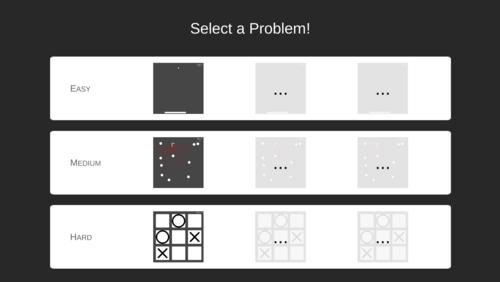
Lernumgebung für Reinforcement Learning
Bachelor-Abschlussarbeit

Jonas Wild, Bachelorstudent im Fachbereich Informatik, hat in seiner Bachelorarbeit eine eigene Umgebung zum intuitiven Verständnis von Reinforcement Learning (RI) implementiert.

Zum Projekt

Effiziente Berechnung hochoszillierender Integrale – acoustic single layer potential

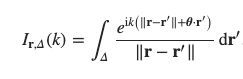
Die numerische Berechnung hochoszillierender Integrale ist ein intensiv studiertes Problem der angewandten Mathematik und ist etwa bei der Simulation hochfrequenter Wellenphänomene wichtig. In der Arbeit „An analysis of the steepest descent method to efficiently compute the three-dimensional acoustic single-layer operator in the high-frequency regime” https://academic.oup.com/imajna/advance-article/doi/10.1093/imanum/drac038/6678755 wird gezeigt, wie eine elegante Methode, welche auf dem Cauchyschen Integralsatz beruht, auf ein wichtiges Flächenintegral im Zusammenhang der Simulation elektromagnetischer Felder angewendet werden kann.

Tobias Arens hat in seiner Masterarbeit am Fachbereich Informatik der Hochschule Trier eine effiziente Implementierung der Methode aus der obigen Arbeit in C++ umgesetzt, und liefert darüber hinaus auch Schnittstellen zu Matlab und Python. https://github.com/xoniuqe